Esta figura es un fractal. Un fractal es una figura, cualquier figura, que se repite un número infinito de veces.
Un pequeño fragmento de cualquier fractal contiene una figura que es idéntica al fractal completo.
LA CURVA DE KOCH
En 1904 el matemático sueco Niels F. Helge von Koch (1870-1924) construye la curva que lleva su nombre.
Parte de un segmento unidad [0,1], poligonal P0, que divide en tres partes sustituyendo la parte central por los dos segmentos que, junto con dicha parte (anulada), formaría un triángulo equilátero. Se obtiene así la poligonal P1.
A continuación se repite el proceso con cada una de las partes resultantes y se obtiene la poligonal P2. Este proceso se repite indefinidamente obteniéndose en cada etapa k una poligonal de longitud (4/3)k.
La curva de Koch se define como la curva límite de la poligonal Pk cuando k tiende a infinito.
Un gráfico nos ayuda a comprender mejor este concepto: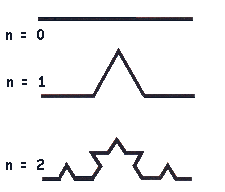
Para crear una curva de Koch click en.
http://omnis.if.ufrj.br/~carlos/applets/koch/koch.html
LA ISLA DE KOCH
Si el iniciador del proceso es un triángulo equilátero y se utiliza como generador la curva de Koch, se obtiene la Isla de Koch o Copo de Nieve cuando n crece indefinidamente.
Luego otros matemáticos se dedicaron a crear variaciones del Copo de Nieve. Veamos:
También son unos fractales muy conocidos, fueron creados por el mnatemático polaco Waclaw Sierpinspi (1882-1969) en 1915. Aquí los tienes:
Pero existen fractales mucho más complejos. ¿Deseas construir un fractal? Aquí tienes el programa DESCARTES:
http://descartes.cnice.mecd.es/Geometria/fractales_igl/fractales.htm
¿Quiéres introducirte en el interior de un fractal? ¡Será un viaje inolvidable!
http://www.fractalus.com/info/zoom.htm
Esta rosa es un fractal. Observala con detenimiento:
posted by Leonardo Sanchez Coello - Conocer Ciencia at 8:15 AM
2 Comments:
WHERE IS THE APPLET FOR HILBER CURVE?
I MEAN HILBERT CURVE
Post a Comment
<< Home