INTRODUCCIÓN

A LA GEOMETRÍA

TÉRMINOS INDEFINIDOS

DE LA GEOMETRÍA:

(PUNTO, LÍNEA Y PLANO)

PUNTO
Un punto sólo tiene posición en el espacio.
Es la unidad indivisible de la geometría.
No tiene dimensión (largo, alto, ancho)



LÍNEA
Línea es una figura geométrica que se genera por un punto en movimiento.




LÍNEA RECTA
Si el punto se mueve sin cambiar de dirección, entonces es una línea recta.

¿LA RECTA ES INFINITA?
Claro las rectas son infinitas por eso en geometría se trbaja con "pedazos" o "trozos" de recta denominados: segmentos de recta.





¿CÓMO UNIR DOS PUNTOS?
Para unir dos puntos, podemos utilizar muchos tipos diferentes de líneas. De todas ellas, la más corta será la línea recta. Una recta está formada por infinitos puntos y no tiene principio ni fin.




LÍNEA CURVA
Si el punto cambia continuamente de dirección entonces es una línea curva.

Una línea puede ser recta, curva o combinada. Una línea cualquiera, puede extenderse en forma ilimitada.




EL PLANO
Un plano es una superficie que tiene longitud y anchura pero no espesor.

El plano tiene dos dimensiones a diferencia de la mayoría de los casos que nos rodean que están en tres dimensiones.

La geometría plana estudia por ejemplo los triángulos, cuadriláteros, circunferencia, círculo...
En otras palabras la geometría plana estudia a las figuras planas (polígonos).





DIAGRAMAS CARTESIANOS



Estos diagramas fueron creados por Rene Descartes, tambien conocido como Cartesio, de ahí que estos diagramas se llamen denominen diagramas cartesianos.

Un diagrama cartesiano consiste en dividir el plano en cuatro partes llamadas cuadrantes mediante dos rectas perpendiculares entre sí (horizontal y vertical respectivamente). Dichas rectas se cortan en un punto que recibe el nombre de origen de coordenadas.

Estas rectas reciben los nombres de: la recta horizontal (llamada "eje de abscisas" o "eje de las x") y la recta vertical (llamada "eje de ordenadas" o "eje de las y").

¿Qué es un par ordenado?



Veamos un ejemplo, en la figura de arriba: el punto de coordenadas (2,3) se localiza situándonos en el punto marcado con el 2 en el eje de las "x"; una vez aquí, subimos hacia arriba verticalmente de forma paralela al eje de las "y", hasta el lugar marcado en este eje con el 3, ese es el punto buscado.


¿Qué es un producto cartesiano?

Si tenemos dos conjuntos A y B, y tratamos de armar todos los pares posibles formados por un elemento del conjunto A y un elemento del conjunto B, obtendremos el producto cartesiano de los dos conjuntos. Se escribe:

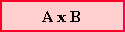
Podemos representarlo de diferentes formas: diagramas de flechas, diagramas arbolados, tablas y gráficos cartesianos. Cada par que formemos con un elemento de A y uno de B, en ese orden, recibe el nombre de par ordenado.

LOS ÁNGULOS

La palabra ángulo proviene de la palabra "rodilla" en griego.

Un ángulo es la porción de plano limitada por dos semirrectas con origen en un mismo punto. Las semirrectas se llaman lado inicial y final. Al origen común se le denomina vértice del ángulo. Un ángulo puede estar situado en cualquier parte del plano pero, a veces nos será útil trasladarlo a un sistema cartesiano de coordenadas de modo que el vértice del ángulo caiga sobre el origen de coordenadas y el lado inicial sobre el eje positivo de abscisas.

Dos semirrectas forman un ángulo. El punto A es el vértice.

El ángulo se denota con una de las letras del alfabeto griego.

Conoce el alfabeto griego:

http://personal5.iddeo.es/ztt/pra/alfabeto_griego.htm

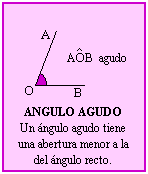
CLASES DE ÁNGULOS

El ángulo que mide 90º se denomina recto. El que mide menos de 90º es un angilo agudo y el que mide más de 90º es un ángulo obtuso. Los ángulos llanos miden 180º.

Pero puedes medir los ángulos con tu puño ¿no lo crees? Click en:

http://www.experimentar.gov.ar/newexperi/NOTAS/planetatierra/lunaexploracion.htm

El sistema sexagésimal

Para medir los ángulos utilizamos el sistema sexagesimal ¿en qué cocnsiste este sistema?. Este sistema ya se conocia en la antigua Babilonia y consiste en dividir un círculo en 360 partes iguales. Cada una de estas partes se denomina grado (º). La cuarta parte, o sea un cuadrante, medirá 90º ¡Sencillo! ¿No?

Para medir los ángulos se emplea el transportador.

Pero puedes fabricar un "transportador de papel" que te servirá, en casos de emergencia, para medir algunos ángulos. Clic en.

http://www.cientec.or.cr/matematica/origami/transportador.html

Construyendo un geoplano

Tupuedes tocar las líneas, construir tus propios polígonos y con0ocer las áreas de los cuadrados, rectángulos y triángulos... sólo tienes que construir un geoplano.

Necesitas una tabla de unos 30x30 cms. Debes de realizar, con un lápiz, un cuadriculado en la tabla (de 6x6, 7x7x, 8x8, dependiendo del tamaño de la madera que tengas). Luego debes de colocar un clavito en cada una de las intersecciones. Ahora puedes construir los polígonos que desees con ligas de colores... ¡Eso es todo! ¡Sencillo y muy útil!

Descarga un geoplano virtual en:

http://www.colombiaaprende.edu.co/html/mediateca/1607/article-73593.html

Debes de tener el programa Win Zip.