LA HISTORIA

Y LA GEOMETRÍA

(II)

EL SISTEMATIZADOR

- EUCLIDES -

Poco se sabe de este matemático griego, incluso hay quien opina que en realidad nunca existió, sino que sus obras pertenecen a un grupo de matemáticos griegos que se hacía llamar por ese nombre. Se cree que vivió entre los siglos IV y III de antes de nuestra era (330-275 A.c) y que trabajó en la Biblioteca de Alejandría. Su gran mérito consistió en recopilar y sintetizar los conocimientos geométricos de su época.

Su libro clave es el llamado Elementos, y constaba originalmente de trece volúmenes en los que se exponía la geometría clásica. Este libro tiene tanta importancia para las matemáticas como el Principia de Newton para la Física o el Origen de las Especies de Darwin para la Biología.

Una página de su primera edición impresa

Para sentar las bases de la Geometría, Euclides utilizó lo que se llama axiomas, que no son otra cosa que principios fundamentales indemostrables pero que se consideran evidentes, y a partir de los cuales se construye una teoría. Él los llamó postulados y formuló cinco primordiales que se pueden exponer de varias maneras equivalentes, una de las cuales es:

1. Si tenemos dos puntos, entonces podemos dibujar una recta que los une
2. Cualquier recta se puede hacer todo lo larga que se quiera
3. Se puede trazar una circunferencia de cualquier tamaño alrededor de cualquier punto
4. Todos los ángulos rectos son iguales
5. Si tenemos una recta y un punto externo a ella, podremos dibujar todas las rectas que queramos qe pasen por ese punto, pero sólo una de ellas será paralela a la que ya teníamos.

Todo esto parece evidente, pero el gran mérito de Euclides fue deducir toda la geometría de su época a partir de estos 5 postulados. Tanto es así, que a la geometría clásica se le llama en su honor Geometría Euclídea o Euclidiana.

El quinto postulado siempre fue polémico, Muchos pensaban que no era un axioma sino un teorema, es decir, parecía que no era tan primordial como los otros y que se podía deducir a partir de los otros 4, y durante siglos se intentó hallar la manera de hacerlo. Sin embargo, resultó que no era posible.

GEOMETRÍAS NO-EUCLIDEANAS

- LOBACHEVSKY -

Pasaron más de 2000 años hasta que el problema del quinto postulado quedó zanjado. Se cree que Karl Fiedrich Gauss (1777- 1885), fue el primero que lo vio claro, pero ni alguien como él, considerado ya en vida uno de los mayores matemáticos de todos los tiempos, se atrevió a publicar sus conclusiones, puesto que rompían con un dogma milenario.

Sí se atrevió un contemporáneo suyo, el ruso Nicolai Lobachevski (1792-1856), quien en 1826 no sólo dijo que el quinto axioma de Euclides no se podía deducir de los otros cuatro, sino que no era tal axioma. Ese axioma se podía sustituir por otro y construir toda una geometría distinta. Sin embargo, la obra de Lovachevski no alcanzó demasiada repercusión más allá de su círculo cercano, en la remota Universidad de Kazán, ciudad perteneciente a la no menos remota república rusa de Tatarstán.



Así surgieron varias geometrías distintas a la clásica, incluso un alumno de Gauss, Georg Bernhard Riemann (1826 – 1866) elaboró una geometría en la que no hay rectas paralelas. El mismo Riemann sintetizó más adelante el estudio de geometrías no euclídeas, llamadas hoy en su honor Geometrías Riemannianas.

¿PUEDEN EXISTIR GEOMETRÍAS NO EUCLIDEAS?

Puede resultar extraño imaginar geometrías en las que no se cumplan los postulados de Euclides, pero hay un ejemplo que nos puede ayudar a imaginarlo, basta con pensar en una esfera, como puede ser un balón de fútbol o, aproximadamente, nuestro planeta Tierra. Si dibujamos una recta sobre esta esfera, ésta no podrá ser infinita como en un plano, puesto que acabaremos volviendo al mismo punto, y por tanto su tamaño será el del diámetro de la esfera, es decir, que no tendremos rectas en el sentido tradicional, sino que tendremos circunferencias que cumplen la misma función que las rectas en la geometría tradicional.

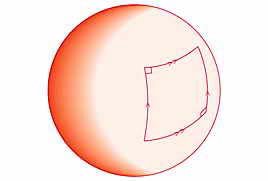
En una esfera la geometría no es igual que en un plano

Este asunto de la esfera se conocía, como es lógico, desde mucho tiempo atrás pero nadie se había puesto a estudiarlo seriamente, se consideraba que sólo eran casos degenerados de geometría euclídea. Sin embargo desde el Siglo XIX se consideran geometrías tan válidas como la clásica, y podemos decir que existen infinitas geometrías posibles, dependiendo de la curvatura de la superficie con la que estemos tratando. La geometría euclídea sólo es el caso particular que se inscribe en un plano, es decir, cuando la curvatura es nula.

LA GEOMETRÍA Y LA RELATIVIDAD

- ALBERT EINSTEIN -

Recordemos que vivimos en un universo de cuatro dimensiones, las tres espaciales más el tiempo. Este asunto de la curvatura del espacio-tiempo se puede imaginar más fácilmente sobre un supuesto universo de sólo dos dimensiones, es decir un plano, como podría ser un colchón. Si en ese colchón se pone una canica, esta se quedará quieta. Pero si después de la canica ponemos un objeto más pesado, como una bola grande de hierro, esta hundirá (curvará) el colchón de forma que la canica tenderá a acercarse a la bola de hierro.

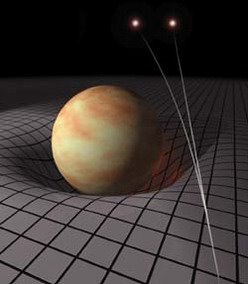
El espacio se curva alrededor de los cuerpos

Se puede decir que la curvatura del colchón es un ejemplo en dos dimensiones de cómo la Tierra curva el espacio a su alrededor atrayendo a los objetos.

Y fue a encontrar el funcionamiento de este espacio curvo a lo que dedicó Einstein ocho años. Las complejas ecuaciones resultantes se podrían resumir así: La curvatura del espacio-tiempo en una zona del universo es igual al contenido de masa y energía de esa región.

La geometría que subyace en esa curvatura no es la de Euclides, sino una no euclidiana que supone consecuencias que nos dan explicaciones distintas para fenómenos que hasta entonces se creían comprendidos. Por ejemplo, los planetas que giran alrededor del Sol en realidad están describiendo una línea recta, pero, como vimos antes, una recta en un espacio no euclidiano es distinta de las rectas de toda la vida.

LOS PROBLEMAS DEL FUTURO

- D. HILBERT -

Matemático alemán. Durante el siglo XIX se puso de manifiesto, cada vez de una manera más evidente, que Euclides no había partido de conceptos patentes y que había supuesto muchas cosas sin especificarlas. Se hicieron esfuerzos para fijar un número mínimo de términos y definiciones básicas sin identificar y de éstas deducir rigurosamente la estructura matemática completa.

Esta es la ciencia axiomática, y fueron Hilbert y Peano quienes la fundaron. Hilbert publicó en 1899 "Foundations of Geometry" (Fundamentos de Geometría), en la que por primera vez se exponían satisfactoriamente una serie de axiomas de geometría. Hilbert se contentó con definir ciertas propiedades en vez de definirlas. También probó que su sistema de axiomas era bastante completo, algo que los griegos habían admitido de los axiomas de Euclides, pero sin demostrarlo. Así completó el trabajo de Euclides sin efectuar cambios en la esencia, pero su fundamento pasó de intuitivo a lógico.

Es famosa la conferencia que dio en el Congreso Internacional de Matemáticas de París en 1900, de título Problemas matemáticos, en la que proponía una lista de 23 problemas que estaban sin resolver (algunos todavía lo están).

Una de estas cuestiones era: ¿son las matemáticas decidibles? es decir, ¿hay un método definido que pueda aplicarse a cualquier sentencia matemática y que nos diga si esa sentencia es cierta o no?. Esta cuestión recibió el nombre de enstcheidungsproblem y para resolverla, Alan Turing construyó, en 1936, un modelo formal de computador, la Máquina de Turing, y demostró que había problemas tales que una máquina no podía resolver.

Otras dos cuestiones: ¿es la matemática completa?, es decir, ¿puede ser demostrada o refutada cualquier sentencia matemática? y ¿es la matemática consistente?, es decir, ¿es cierto que sentencias tales como 0 = 1 no pueden demostrarse por métodos válidos?. En 1931, Kurt Gödel fue capaz de responder a estas dos preguntas, demostrando que cualquier sistema formal suficientemente potente es inconsistente o incompleto.

Hilbert trabajó sobre los invariantes algebraicos, geometría (su libro Los fundamentos de la Geometría es un clásico), ecuaciones integrales, también se dedicó a la Física (decía que la Física es demasiado difícil para los físicos), su libro Los métodos de la Física matemática, de Richard Courant y David Hilbert (se conoce como el Courant-Hilbert) se sigue imprimiendo en la actualidad; también trabajo en los fundamentos de las matemáticas y en la lógica matemática.

El epitafio de Hilbert es "Wir müssen wissen, wir werden wissen" ("Debemos saber, de modo que sabremos")